Great Martingale
Strategy principles
The Great Martingale is based on the same rules of the Classic Martingale with one difference, the player must add a bet unit each time he loses. Besides covering the losses, this strategy allows to recover the potential profit of lost bets.
The Great Martingale was created in response to a weakness of the original strategy, the profits received following a win at the end of a series of losses is ridiculous compared to the risks taken with high amounts of bets. At the end of a serie of losses, in addition to winning the last bet, the Great Martingale can recover the potential winnings of all losses in the serie.
This method solves a problem of the Classic Martingale but aggravates its main disadvantage; the exponential rise in stakes. It has often precipitated bankruptcy of gamblers.
Rules of the Great Martingale
Although it can be applied to any type of gambling; sports, horse racing or even in trading, the Great Martingale is popular in casinos and especially in roulette in simple bets (red / black, pair / odd …).
Two simple rules :
- Multiply the bet after each loss as in the Classic Martingale and add in addition a base bet unit. In a classic roulette case where odds are 2 (+100), the gambler should double his bet after each loss and add a bet unit.
- Return to a base bet unit after a win.
Example
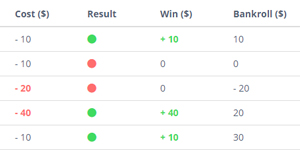
In this example simulated on GSimulator, played Odds are 2 (US +100), probability 50% and the bet unit is $10 :
| # | Cost ($) | Result | Win ($) | Bankroll ($) |
|---|---|---|---|---|
| 1 | – 10 | 10 | 10 | |
| 2 | – 10 | 0 | 0 | |
| 3 | – 30 | 0 | – 30 | |
| 4 | – 70 | 0 | – 100 | |
| 5 | – 150 | 0 | – 250 | |
| 6 | – 310 | 310 | 60 | |
| 7 | 10 | 10 | 70 |
- In this example the martingale is triggered from the second iteration following a loss.
- The gambler doubles the bet and adds a bet unit after each loss until the next win. In this example, following the sixth round, the player recovers all of his last four losses 10 + 30 + 70 + 150 = $260, in addition to the profit of one base bet unit per wager 5 * 10 = $50. That makes a total of 260 + 50 = $310.
- In this example, $310 were needed to continue playing after four consecutive losses. If the sixth bet was losing, the gambler would have had to play $630 at the next round!
Benefits and risks
The Great Martingale aims to secure higher earnings. Following a seri of losses, the addition of an additional wagering unit each time would allow the next winning bet to recover the potential winnings of all previous losses. Compared to the Classic Martingale, after 10 consecutive losses, the classic martingale recovers the lost bets plus the profit of only the last winning bet, but the Great Martingale would also recover the potential winnings of the last 10 lost bets.
This compensation has a higher cost. The Great Martingale has the same risks of bankruptcy following large black series, the addition of bet units will only accelerate the increasing of the bet.
Another very important limitation is that casinos and sports betting sites impose limits on maximum bets, even if the gambler has a very high or an unlimited bankroll, he will find himself stuck with this limitation and will not be able to cover big losses.
GSimulator
The apparent simplicity of the martingales hides a complexity and a subtlety due to the multitude of parameters that can spectacularly change the results, the number of repetitions, the available bankroll, the amount of bets and especially the odds… GSimulator allows to generate a gambling-weighted random distribution, calculates the results, and provide tools to analyze and understand the behavior of betting systems in different situations. You can use the simulator to estimate the variation of the costs between the Classic Martingale and the Great Martingale for example.
Start a free simulation of the Great Martingale strategy in the GSimulator or consult the documentation for more informations.
Other betting systems
Other strategies and betting systems exist and try to limit the losses, or to increase the profit, by making changes to the rules of stakes following the losses (negative progression) or following the wins (positive progression) :
- Classic Martingale
Increase stake after every loss - Fibonacci (Whittacker)
Increase and decrease stake based on the Fibonacci sequence - Reverse Martingale (Paroli)
Increase stake after winning until stop limit - d’Alembert
Increase stakes after a loss, descrease after a win - Contra d’Alembert
Increase stakes after a win, descrease after a loss - Labouchère
Remove first and last number in the Labouchere sequence after a win, add the last bet to the sequence after a loss - Reverse Labouchère
Remove first and last number in the Labouchere sequence after a loss, add the last bet to the sequence after a win